Entropy, Mutual Information, KL divergence
Information theory
Information theory is a branch of applied mathematics that revolves around quantifying how much information is present in a signal.
Basics
Consider 2 messages:
A: it is dark tonightB: it is a blood moon tonight
Message A is plainly uninformative. Almost every night is a dark night. Message B is an unlikely event that gives us more information content. A blood moons occurs every few years.
Therefore we want to quantify information such that more unlikely events have higher information content. The more surprised we are of an event occurring, the more information content.
The self-information of an event is:
I(x) = -log_{2}(p(x)) bits
If I throw a fair coin how surprised will we be when it lands heads?
I(H) = -log_{2}(0.5) = 1 bit
What if our coin is unfair? Consider
p(H) = 0.99, p(T) = 0.01 being probabilities of landing heads and tails respectively.
Then:
I(H) = -log_{2}{0.99} = 0.014 bits
and
I(T) = -log_{2}{0.01} = 0.014 = 6.64 bits
We see that more unlikely events contain more information.
Entropy
If we keep throwing the coin, we generate more information. How much information is produced on average? In other words what is the expected value of information content? That's entropy.
Entropy quantifies the amount of uncertainty/surprise/information involved in a random variable/process.
Hence:
H(X) = E[I(X)] = E[-log_2(p(X))] = -\sum_{x \in X} p(x)log_2(p(x))
In our fair coin this would be:
H(X_{fair}) = - (0.5log(0.5) + 0.5log(0.5)) = 1 bit
whereas
H(X_{unfair}) = - (0.99log(0.99) + 0.01log(0.91)) = 0.08 bits
Consider fair n-sides dices:
H(X_{fair_{n}}) = -n*(\frac{1}{n}log(\frac{1}{n})) = -log(\frac{1}{n})
| n | information |
|---|---|
| 2 | 1 bit |
| 4 | 2 bits |
| 8 | 3 bits |
| . | . |
Therefore, the more spread out the events in our random variable or process, the more the expected uncertainty, the more the information content. Intuitively, you are surprised less often when you know the coin is almost always heads. Information gained = reducing expected uncertainty = reducing expected information content = less bits required to encode = ....
How does this translate to signals/messages in information theory?
For example, a 2-side die (coin) has entropy 1, which means the amount of information needed to specify the value of the coin is 1 bit. Therefore it may be encoded in a message as \{side_1: 0, side_2: 1\}, which is precisely 1 bit. So a message of 3 coin tosses may look like this: 011. In a 4-sided die we encode it as \{side_1 : 00, side_2 : 01, side_3 : 10, side_4: 11 \}. So 3 coin tosses may look like this: 001011.
Notes:
- I use
$H(X) = H(p(x)) = H(p)$interchangeably for random variable X with outcomes x_i, and probability distribution x \sim p(x)
Joint and Conditional Entropy
Consider a joint distribution f(X,Y) between X and Y random variables.
The joint entropy may be defined as: H(X, Y) = - \sum_{x \in X} \sum_{y \in Y} p(x, y) log_{2}(p(x, y))
Joint entropy: joint expected uncertainty/joint expected information content.
Similarly the conditional entropy, H(Y|X) is equivalent to:
H(Y|X) = \sum_{x \in X} p(x)H(Y | X = x) = - \sum_{x \in X} \sum_{y \in Y} p(x, y) log_{2}(p(y|x))
Conditional entropy: how much more uncertainty/information content remains in Y having observed X - for H(Y|X)
Notes:
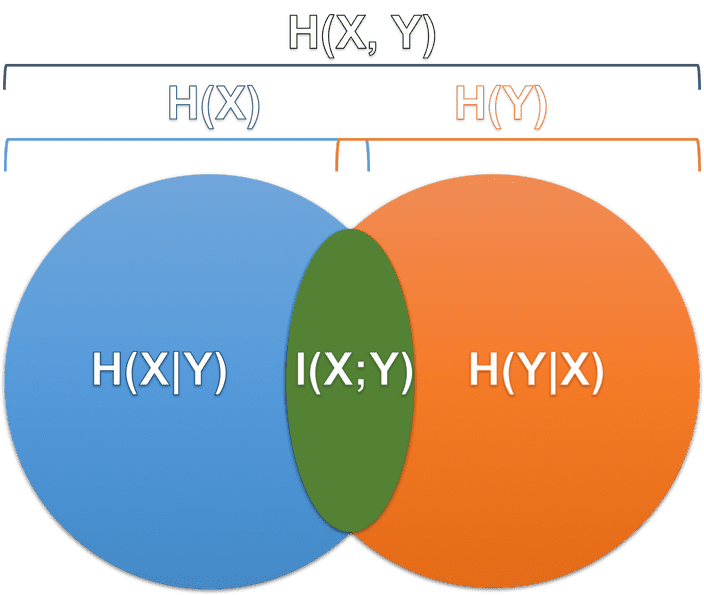
We may apply the chain rule as follows: H(X, Y) = H(X | Y) + H(Y) = H(Y | X) + H(X)
if X and Y are
independentthen H(Y|X) = H(Y), that is, knowing about X does not change entropy of Y$H(Y|X) \neq H(X|Y)
Mutual Information
Mutual information is the information gain/uncertainty reduction in X after we know Y, or vice versa.
Note the difference between conditional entropy and mutual information. In conditional entropy it is how much uncertainty remains in X given Y; in mutual information it is how much uncertainty is reduced in X given Y.
Looking at the image below, we can clearly see that this is I(X;Y).
Therefore:
I(X;Y) = \sum_{x,y} p(x,y) log_2(\frac{p(x,y)}{p(x)p(y)})
As:
Notes:
- I(X; X) = H(X) - knowing X gives you all the information about X
- Mutual information is
symmetric
KL divergence and cross entropy
Recall entropy:
Now we want to measure the 'relatedness' between distributions p(x) and q(x). Let p(x) be the true underlying distribution and q(x) our approximate. The cross entropy is defined as:
The cross entropy between p(x) and q(x) is the average number of bits (using log_2) needed to encode an event x if we used the approximate distribution x ~ q(x) instead of x ~ p(x).
For example if we are approximating a fair coin toss:
Therefore for H(p, q) we require 1.029 bits to encode an event in x \sim p(x) using distribution q. In comparison for, H(p, p), as expected, we require 1 bit to encode an event in x \sim p(x) using the true distribution p. Therefore 0.029 extra bits are required from distribution q to encode an event in x compared to distribution p.
Therefore:
H(p, q) - H(p, p) = 0.029 bits
This is the Kullback-Leibler (KL) divergence. By definition the KL-divergence FROM p TO q is:
Therefore cross entropy between distributions p and q may be written as:
H(p, q) = H(p) + KL(p || q) = \sum_{x} p(x) log_2( q(x))
In summary:
- H( p ) - Average number of bits to represent an event.
- KL(p || q) - Average number of extra bits to represent an event with q instead of p
- H(p, q) - Average number of bits to represent an event with q instead of p
Notes:
Cross entropy is used as a loss function in classification problems.
KL divergence is
asymmetric. KL(q || p) \neq KL(p || q).Mutual information may be written as the KL-divergence FROM joint distribution TO product of marginals:
I(X;Y) = KL(p(x,y) || p(x)p(y))So pretty much how many
extrabits are needed to represent an event from the true distribution p = (joint distribution X,Y) using a distribution q = (product of marginals X,Y) is equivalent to how much information (in bits) isobtainedabout one random variable (e.g. X) having observed the other (e.g. Y).IfX and Y areindependentthen KL divergence is 0 as no extra bits are needed. Similarly mutual information is 0 as no information can be obtained after observing an independent random variable.